考虑了具有多种请求类型和限制处理器共享的优先级队列模型。提出了一种新的请求、接纳和服务学科。该原则假定服务器的带宽(容量)和系统中可以同时接收服务的请求数量受到限制。这门学科是传统的多服务器系统服务学科和有限处理器共享学科的某种现实混合。最高优先级的请求可以从服务中推出低优先级的请求。因此,重要的问题是将可以同时接收服务的请求数量与服务器的带宽相匹配。通过构造和分析描述系统在任意一组固定参数下的运行的多维马尔可夫链来解决这一问题。
排队理论是一种被广泛认可的数学工具,用于解决在用户竞争请求中资源分配受限的任务的最优解。最简单的模型假设按一定顺序依次向客户提供服务,一个接一个。更一般的模型提出了某种资源共享和同时为多个请求提供服务的可能性。管理多个请求的同时服务的两个最流行的原则如下:一个资源被分成几个部分(称为服务器),每个接收服务的请求使用分配给他/她的服务器。请求的服务时间是独立的。我们将这种系统称为多服务器系统;b资源由所有请求共同使用,服务率与接收服务的请求数成反比。这个原则被称为处理器共享(PS)。关于与这一学科相关的研究调查及其一些概括,见(Yashkov 1987;Yashkov and Yashkova 2007;Altman et al. 2006)。
现有的绝大多数研究,从A.K. Erlang的开创性作品开始,假设学科A.具有无限或有限缓冲、损失、重审及其部分情况的类型(在D.G. Kendall的符号中)的排队模型进行了足够充分的扩展,特别是在服务时间具有指数分布的情况下。对于服务时间具有任意G分布的模型,只进行了近似或渐近的研究。特别地,对某些性能特性得到了一定的界限。
A学科的一个优点是相对容易实现。例如,在呼叫中心,几个接线员可以使用单独的工作站和通信通道向用户提供服务。在信息传输系统中,物理资源,例如信道的带宽,可以划分(使用各种技术方案,如频分、时分、码分多路复用等)为逻辑信道(服务器),每个信道被分配给一个单独的请求服务。学科A的明显缺点是资源可能得不到充分利用。只有少数逻辑通道处于繁忙状态,而其他通道处于空闲状态。
PS学科没有这个缺点。如果有服务请求,资源(让我们进一步称其为带宽)总是被充分使用。然而,在许多具体应用中,除了与带宽动态再分配的必要性相关的更困难的技术实现外,PS学科本质上的两个缺点如下:
(i)
当当前系统中呈现的请求不需要全部带宽时,就有可能出现这种情况。例如,如果五个呈现用户需要以每秒10兆比特(Mbps)的速率传输他们的信息,他们不需要完全共享100mbps信道的可用带宽。他们总共只使用50mbps;
(2)
用户对分配给他/她的带宽可能存在一些最低要求。例如,用户可能要求MPEG2传输流中高清内容的视频点播传输带宽为12mbps,但由于服务质量较差而不同意使用较小的带宽。因此,100mbps通道的同时服务用户数必须小于9。因此,假设所有到达的请求都被服务接受的纯PS原则不适用于所考虑的传输过程的建模。
作为克服缺点(ii)的工具,文献中提供了有限PS (LPS)的学科。这一学科表明,同时使用带宽的用户数量受到某个有限数字的限制,比如n。这个数字有时被称为多道编程级别,参见,例如(Nair等人,2010),或者并发限制,参见,例如(Gupta和Zhang, 2022)。相关文献请参见(Alencar et al. 2021;Telek and Van Houdt 2018;Samouylov et al. 2016;Dudin et al. 2017;Masuyama and Takine 2003;Dudin et al. 2021;Ghosh and Banik 2017;Bocharov et al. 2007;Brugno et al. 2017,2018;D 'Arienzo et al. 2020;Kim et al. 2019)。
本文的贡献包括以下内容。
我们提出了一种新的混合学科,称为受限处理器共享。该学科结合了学科A和学科b的积极特征。在学科A和学科LPS中,我们假设可以同时接收服务的最大请求数为整数。在学科A中,N对应服务器的数量。在LPS规程中,N对应于并发限制。如果到达的请求在服务中遇到N个请求,在本文中我们假设它丢失了。当这样的请求被排队到无限或有限的缓冲区中,或将使重试的变量,将根据下面对丢失请求的系统的分析结果,留给未来的研究。描述系统行为的多维马尔可夫链生成器的块的推导表达式可以作为描述具有缓冲和重试的系统动力学的马尔可夫链生成器形式的推导的基础。混合规则假定与每个请求相关联的是所需的工作量(信息量)和所需的(名义)服务速率。停留在系统中的所有请求的总服务速率受到参数B(称为服务器带宽)的限制。如果停留在系统中的所有请求的名义服务速率之和不超过带宽,则所有请求以名义速率相互独立地接受服务,如规则a。如果停留在系统中的请求的名义服务速率之和超过带宽,则所有请求以按比例降低的速率接受服务,如规则LPS。
我们建议请求在重要性、所需带宽和名义服务方面是异构的。请求的类型是有限的M种。不同类型的请求具有不同的优先级。其中一种类型的请求比其他类型的请求具有优先级。当获得服务的请求数量等于N时,这种请求的到达意味着系统中呈现的优先级最低的请求(如果有的话)中的一个丢失。为了降低低优先级请求中断服务的概率,当接收服务的请求数小于N但超过一定的阈值时,系统将不接受低优先级请求。所考虑的模型可以具有广泛的应用领域。当只有两种类型的请求时,这种特殊情况非常适合对认知无线电系统进行建模。Type-1请求由主(许可)用户发送。Type-2请求由认知(辅助)用户发送。值得注意的是,现有的文献模型,见,例如(El-Toukhy and Arslan 2019;Goel and Kulshrestha 2022;Sun等,2014,b, a;Lee et al. 2022)的认知无线电系统是我们模型的特殊情况,具有和不具有以降低速率服务请求的可能性。
虽然绝大多数或多或少相关的论文假设请求流被定义为平稳的泊松到达过程,但在这里,我们假设到达的异构流由标记马尔可夫到达过程(MMAP)描述(参见,例如(He 1996))。这允许充分考虑突发性质(高可变性和连续间隔到达时间的依赖性),这是各种现代电信网络、联络中心等信息流的固有特征,参见(Chen et al. 2022),其中呈现了有关真实流动轨迹的信息。值得注意的是,使用平稳泊松到达过程作为实际过程的模型通常意味着对系统性能指标的估计过于乐观。
本文的提示如下。在第2节中,描述了考虑的数学模型。描述所研究模型行为的马尔可夫过程在第3节中进行了定义和分析。系统基本性能指标的计算表达式见第4节。在第5节中,给出了一个数值例子。第6节是本文的简短结论。
我们考虑一个具有受限处理器共享规则的排队系统。系统方案如图1所示。
图1
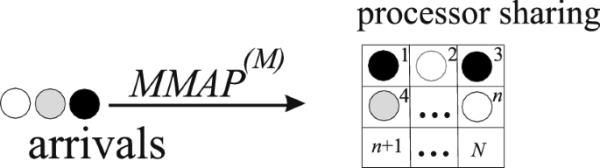
系统结构
进入系统的请求分为M种类型。请求的到达由MMAP描述,参见(He 1996)。该过程是一个具有有限状态空间的连续时间马尔可夫链,该马尔可夫链的过渡速率由不可约生成器D决定,矩阵D被分解为矩阵和,矩阵的元素决定马尔可夫链的过渡速率,并伴随着m类型请求的生成。矩阵中的非对角项决定了马尔可夫链的转换速率,这并不伴随着请求的生成。矩阵负对角元素的模决定了马尔可夫链从相应状态退出的速率。
类型m的请求到达的平均强度由式给出,其中为过程不变概率的行向量,定义为具有归一化条件的线性代数方程组的唯一解。这里是一个适当大小的列向量,由1组成,是一个由0组成的行向量。该符号表示参数m允许值。请求的总强度定义为
我们将请求服务解释为一定数量信息的传输。服务器的带宽定义为每单位时间内可以传输的最大兆位数,记为b。我们假设服务器的带宽被所有请求使用。同时服务请求的最大可能数量受参数n的限制,假设服务一个类型为m的请求所传输的信息量随速率呈指数分布,值表示一个类型为m的请求的平均数据量,假设不同类型的请求需要不同的服务强度。用m类型请求所需的比特率表示(标称比特率)。因此,m类型请求的标称服务时间为,因此,m类型请求的标称服务强度计算为:在服务器带宽不短缺的情况下,向任何请求提供所需比特率(标称服务强度),即所有接受服务的请求的期望比特率总和不超过服务器的带宽。否则,提供给所有请求的比特率将相应降低。
我们假设请求具有不同的优先级。第一类请求的优先级最高,…,类型M的请求具有最低的优先级。这意味着以下内容。首先,我们假设如果已经服务的请求的数量等于或超过参数,则不接受类型m的请求进入系统。这意味着专门为第一种类型的服务请求保留了位置。如果一个类型1的请求在接收服务的请求数等于N或类型m的请求时到达,当接收服务的请求数不少于且该服务上存在优先级较低的请求时到达,则到达的请求将取代优先级最低的服务请求之一并启动该服务。移位的请求丢失。
设服务上的请求数,为第t时刻接收服务的类型m的请求数,如由于应用了带宽共享原则,只有在第t时刻使用的带宽(定义为小于服务器的带宽B)时,该请求的实际服务强度才等于其名义服务速率。否则,类型m请求的服务率被削减,等于
很明显,这是一个随机过程
在哪里
完全描述了所考虑的排队系统的行为,是一个正则的连续时间马尔可夫链。
由于该马尔可夫链是不可约的,并且具有有限的状态空间,因此已知其极限
对于系统参数的任何值都存在。它们被称为系统状态的平稳概率或稳态概率。
为了简化多维马尔可夫链的分析,将具有组件值n的过程的状态集组合成所谓的层次是有用的。为了确定,我们按照组件的字典顺序和m维过程的组件的反向字典顺序对属于层次的状态进行编号
根据这个枚举,我们将属于n层状态的平稳概率组合成行向量,这些向量满足线性代数方程组(平衡方程)。
(1)
式中,A为马尔可夫链的无穷小发生器,其归一化条件为:
为了求解该系统,需要获得生成器a。这样,最困难的特殊问题是描述m维过程中决定系统中每种类型请求当前数量的组件的转换强度。要计算这些强度,首先我们需要在系统没有过度拥挤并且请求永久接收所需的名义服务率时正式定义请求服务的过程。分析各种场景,可以确定这种请求的服务时间具有所谓的广义相位类型(GPH)分布,参见(Dudin et al. 2016)。这种分布是将文献中众所周知的阶段类型分布(参见Neuts 1981)推广到异构请求服务的情况。GPH分布的基本思想是避免在服务期间监视每个请求的类型。它是通过使用不同的概率向量来安装不同类型请求的底层服务过程的初始状态,以及使用公共子生成器来描述其状态空间内底层服务过程的转换来实现的。有关GPH分布及其应用示例的更多详细信息,请参见(Dudin et al. 2016)。
作为任意请求服务的底层过程,我们称之为连续时间马尔可夫链,定义如下。链的状态空间是整数的集合,链在请求服务开始时的初始状态是随机选择的,其概率定义为由给出的概率向量的分量
如果此请求为m类型。马尔可夫链到吸收状态的过渡速率由列向量决定,其中子发生器由公式定义,其中表示具有括号中指定的对角元素的对角矩阵。
定义了单个请求的服务时间分布后,我们可以描述多维过程的转换强度。为此,我们将该方法扩展到论文中(Ramaswami和Lucantoni 1985)。我们使用下面的符号。如果系统中的所有n个请求都以名义(未降低)速率接收服务,则设
矩阵定义了新型m请求在服务开始时刻的进程转移概率,;
矩阵)定义了当其中一个请求完成服务时流程的转换强度;
if和if是大小的方阵,它们的元素决定了在请求到达时类型为m的请求到达的概率,当请求收到服务时,或者当有N个请求在服务中时类型为1的请求到达,并且到达的请求试图从服务中取代具有较低优先级的请求。矩阵的每一行中只有一个元素不同于0且等于1。为了定义哪个条目等于1,我们注意到矩阵的每一行和每一列都对应于流程的特定状态。回想一下,流程的所有状态都是按照条目的反向字典顺序编号的。例如,矩阵的第一行和列对应的状态,第二行和列对应的状态,,最后一行和列对应的状态矩阵的行对应的状态,1是放置在列元素对应于相同的状态只有在这种情况下,所有到达的请求类型的m是失去了,因为没有一个低优先级的请求系统。如果对于某些值和是这些值l的最大值,则将元素1放置在与状态对应的列中
在这种情况下,类型请求具有最低的优先级,并且到达的类型m请求取代离开系统的任何类型请求(丢失)。
例如,在(Kim et al. 2013)和(Kim et al. 2021)中,给出了对这些矩阵和计算它们的算法的更详细描述。
考虑到当系统带宽中呈现的所有请求所需带宽之和大于服务器B的带宽时,接收到的服务率降低,我们需要更多的表示法,即:
在哪里
维的列向量,其元素定义为
维的列向量,其元素定义为
一个对角矩阵的对角元素是由向量的元素给出的吗
现在我们准备呈现生成器a。由于每次只有一个请求进入系统并离开,很明显矩阵a具有块-三对角线结构:
对角块的对角元素为负,其模数决定了马尔可夫链偏离相应状态的强度。这些块的非对角线元素是非负的,决定了n层内马尔可夫链的转移强度。矩阵和的元素是非负的,分别决定了从n层到和层的转移率。
块的显式形式如下:
其中为大小为W的单位矩阵,表示矩阵的克罗内克积和和的符号,例如参见(Graham 2018)。
定理1的证明是通过分析无穷小区间内的马尔可夫链跃迁来实现的,在这里略去。请注意,矢量的使用允许考虑在带宽不足的情况下服务速率的降低。
具有块-三对角线结构的链在文献中被称为水平相关的准生-死过程。系统(1)的大小可以很大。对于此类系统的求解,建议利用生成器a的稀疏结构,例如,可以使用(Baumann and Sandmann 2010)的算法。
一旦计算出向量,它们就可以用于计算所分析的排队系统的各种性能指标的值。部分绩效指标的计算公式如下:
系统中的平均请求数为
成功接收到服务的请求输出流的速率等于
(1)
从总概率公式和公式(1)的等价形式可以明显地证明这个公式。
行向量定义了马尔可夫链状态的平稳概率,例如系统中的请求数等于n,列向量的分量定义了马尔可夫链在这些状态中停留期间成功完成服务的比率。
接收到服务的type-m请求的输出流速率等于
在哪里
系统中type-m请求的平均个数为
(2)
该公式的证明与式(1)的证明类似。考虑到乘法器只选择向量中占m类型请求数的分量,且这些请求的离开率等于1,从总概率公式中可以明显地推导出来。因此,式(2)右侧的和定义了系统中m类请求的平均数量。
任意请求在其到达时刻丢失的概率为
哪个对角矩阵和这个矩阵有相同的对角元素
任意类型1请求丢失的概率为
任意类型m请求到达时丢失的概率为
在任意时刻出现带宽短缺的概率等于
在任意时刻所有请求获得所需服务率的概率等于
设大小的方阵中,if和if定义了在接收服务的请求数为n时,第m类请求到达系统并取代第l类请求的时刻,进程的转移概率。该矩阵的定义与上述矩阵的定义类似。在这个矩阵的每一行中,只有一个元素不等于0,而是等于1。我们使用在矩阵定义中提到的事实,即矩阵的每一行和每一列都对应于过程的某一状态。在与状态对应的矩阵的行中,只有当对所有且不满足此条件时,元素1才被放置在与状态对应的列中。
m型要求的位移强度计算为
由于位移导致任意请求丢失的概率等于
由位移引起的任意类型损失请求的概率为
由于类型1请求的位移而导致类型损失的任意请求的概率等于
到达类型客户发出任意类型请求的概率等于
任意请求的丢失概率为
摘要
1 介绍
2 数学模型
3.描述系统动力学的过程
4 性能特征
5 数值例子
6 结论
数据和材料的可用性
参考文献
作者信息
道德声明
搜索
导航
#####
我们假设有三种类型的请求()。请求的大小以兆比特(Mb)为单位。类型m请求的大小与我们设置的速率呈指数分布,因此,类型1客户的平均大小为40mb。类型1请求的标称比特率为20mb / s。对应的,在没有带宽不足的情况下,第1类客户的服务速率为:对于第2类和第3类请求,Mbps和Mbps,
我们假设请求的到达流是由矩阵定义的MMAP
客户的平均总到达强度为m类请求的平均到达强度为,,。到达间隔时间的变异系数为1.52387,m类请求到达间隔时间的变异系数分别为2.32208、1.13619、1.50726。两次连续到达间隔时间的相关系数为0.159857,m类请求两次连续到达间隔时间的相关系数分别为0.236901、0.0466208、0.128633。
我们修正了可以同时获得服务的最大请求数
在这个数值示例中,我们打算研究服务器B的带宽和定义接受低优先级请求的参数对系统主要性能指标的影响。为此,我们在步骤50中改变带宽B的范围[50,300],在步骤1中改变参数的范围[1,50]。计算在PC上实现,CPU为Intel酷睿i7-8700,内存为16gb,软件为Wolfram Mathematica 12.1。300双鞋的运行时间约为80分钟,平均每双鞋运行时间为16秒。
图2显示了系统中请求的平均总数和m类请求的平均数量对参数和B的依赖关系。
图2
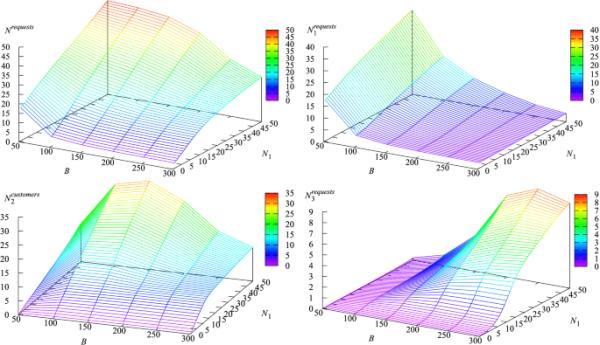
请求的平均数量和参数与B的依赖关系
从图2中可以看出,在所考虑的情况下,平均总请求数随着服务器B带宽的增加而减少,随着参数的增加而增加。在固定情况下,随着带宽B的增加而减少,这是因为随着B的增加,服务速率增加,因此请求更快地离开系统。在固定的B下,随着in的增加而增加,这是由于增加的导致更宽容的接受政策。由于服务器带宽不足,更多的请求被允许进入系统,这可能导致服务速率的降低。系统中类型1请求的数量与系统中请求的总数的行为方式相同。类型2和类型3请求的平均值和也随着带宽b的增加而增加,但其表现不是单调的,这种行为可以解释如下。首先,当B较小时,在到达时刻拒绝了许多类型2和类型3的请求。随着B的增长,服务率增加,系统接受的请求也越来越多,这导致了和的增长。然而,随着B的进一步增长,服务器变得不那么拥挤,这显然导致系统中类型2和类型3请求的平均数量减少。
图3显示了参数和B对损失概率和的影响
图3
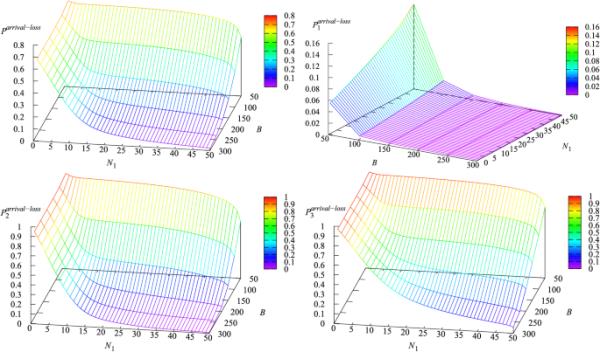
概率对参数和B的依赖性
从图3可以看出,随着带宽B的增长,任何类型请求的丢失概率都在下降,因为带宽越大,平均服务速率越大,请求离开服务器的速度越快,为到达的请求腾出空间。的增加意味着和的损失概率减小,和的损失概率减小。尽管对类型2和类型3的请求具有抢占优先级,但损失概率减小的原因可以解释为:当增加时,系统接受的此类请求显然更多。服务器负载增加,由于共享类型1请求的服务速度降低,一个到达的类型1请求遇到N个获得服务的类型1请求的情况更加频繁。
任意时刻所有请求获得所需服务率的概率与参数和B的依赖关系如图4所示。这个图证实了当B大而B小时概率大。相应的,当B较小和较大时,该概率较小。
图4
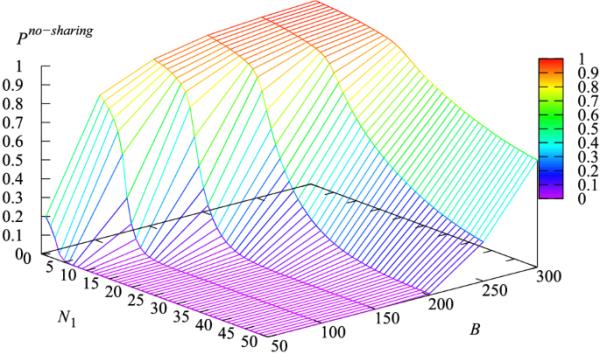
概率对参数和B的依赖
这些观察结果,以及图5、6、7给出的一些相关性是显而易见的。然而,由于模型的复杂性,一些曲线的行为,如图5和图6所示,是相当复杂的。所呈现的图表的有用性包括给出任何固定值B和的重要性能度量的确切值,特别是,这允许解决各种优化问题。
图5
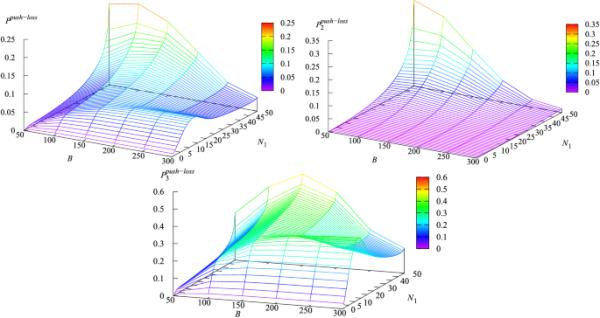
和对参数和B的依赖
图6
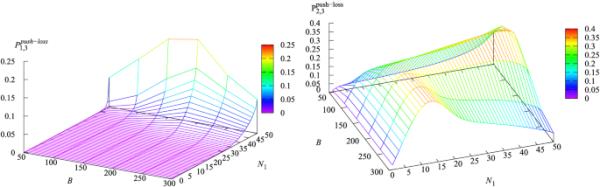
和对参数和B的依赖
图7
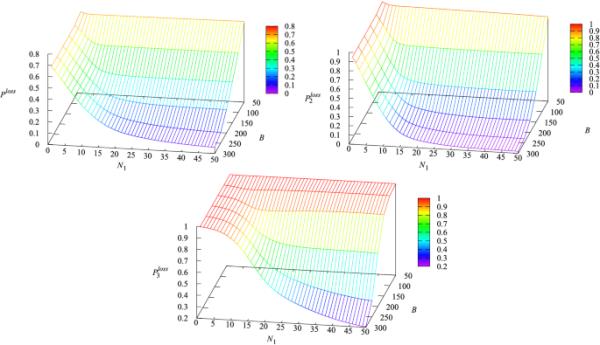
和对参数和B的依赖
现在让我们介绍定义为的成本标准
并通过参数B和的适当选择来考虑该准则的最大化问题
这是服务一种类型的请求所获得的利润;
是一种请求到达时的损失费用;
为因推出而丢失1类m请求的费用;
是单位时间使用单位带宽的费用。
让引入的成本定义为
函数的形状如图8所示。cost准则的最优值为7.82733,带宽B的最优值为200,阈值为27。
图8
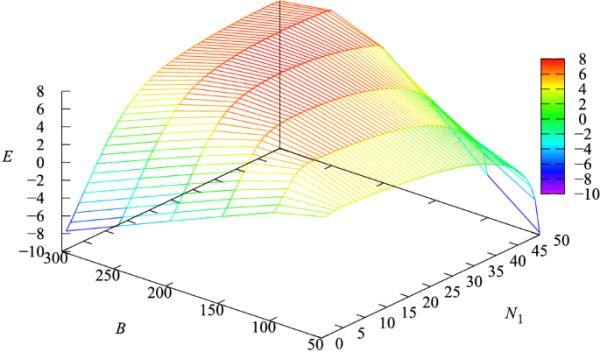
代价函数E对参数和B的依赖性
本文介绍并分析了一种新的多请求同时服务学科。这一学科看起来在现实世界系统中的应用是现实的。它假定对服务器的带宽和可以同时接收服务的请求数量有限制。当系统中呈现的请求数量相对较少时,每个请求都获得永久的带宽共享,并且它们的服务进程相互独立,就像标准的多服务器排队系统中的服务一样。但是,当系统接收的请求的带宽总和超过服务器的带宽时,将按比例降低的速率为请求提供服务。就服务速率的需求而言,请求是异构的,并且具有不同的优先级。其中一种类型的请求具有优先于所有其他类型的请求的优先权,并且在系统中呈现的请求数量达到最大可接受值之前,不受允许限制。其他类型的请求在允许方面有更严格的限制,并且彼此具有抢占优先级。
模型的分析是在实际的相关性和可能的高变异性下进行的。这是通过假设到达根据MMAP过程发生来实现的,MMAP过程本质上是比固定泊松过程的叠加更一般的到达过程。数值算例说明了所提分析方法的可行性。特别给出了服务器带宽最优值和可同时接收服务的请求数计算问题的解决结果。由于该技术的应用可以追溯到D. Lucantoni和W. Ramaswami的作品,因此可以实现计算,而不仅仅是同时接收相对较少数量的请求。
所考虑的模型表明,当服务下的请求数量达到最大值时,到达的请求会丢失。所提供的分析计划扩展到将此类请求存储在无限或有限缓冲区中或可能重复尝试进入服务的场景。在这些情况下,系统的运行可以用马尔可夫链来描述,其中为轨道缓冲区中的请求数,为本文分析的马尔可夫链。如果链的状态按直接字典顺序枚举,链的层次由组件的固定值定义,那么本文所分析的马尔可夫链生成器的区块就可以作为马尔可夫链生成器区块的子区块
也可以考虑将不相等的份额分配给竞争请求流的情况,例如(Chen et al. 2022)。可以考虑将所获得的结果应用于供应系统分析的问题,例如(Falco et al. 2017), (Gaeta和rarit
2013)。
下载原文档:https://link.springer.com/content/pdf/10.1007/s12652-022-04233-w.pdf


