我们经常在扔废纸之前把它揉成一团。然而,这个平凡的动作却创造了一个具有惊人机械特性的独特复杂系统。拿一张薄塑料片,比如玻璃纸,自己试一试。普通的薄片在重力的作用下会弯曲,而皱巴巴的薄片更硬,可以承受自身的重量。它也有形状记忆——它有许多稳定的结构,因此会倾向于保持变形后的形状。
特拉维夫大学的Yoav Lahini博士长期以来一直痴迷于研究皱巴巴的薄片。他解释说:“这一点也不稀奇。”“皱巴巴的纸与其他更难以研究的复杂系统有许多共同的奇怪行为。把实验拿在手里的能力可以带来很多直觉。”
在《自然物理学》(Nature Physics)上发表的一项新研究中,拉希尼博士和他的学生多尔·肖哈特(Dor Shohat)和亚尼夫·弗里德曼(Yaniv Friedman)利用皱褶的薄片,对慢松弛和物理老化的机制进行了新的阐释,这是无序系统物理学中一个长期存在的问题。
为了理解这个问题,考虑下面的桌面实验:拿一张薄纸,把它揉成一个球,然后把它放在一个重物下。而不是放松到一个固定的体积,正如人们所期望的那样,揉皱的球将继续在重量下压缩,而不会达到平衡。
20多年前,Kittiwit Matan和他的同事们的实验表明,这种缓慢的压实速度在时间上是对数的,这意味着压实速度在不断减慢,但即使在几周后也没有停止的迹象。
对数松弛并不是皱巴巴的纸所特有的。它们出现在凝聚态物理中各种无序系统中,从聚合物和沙堆到无序导体和玻璃,然而它们的微观起源却知之甚少。
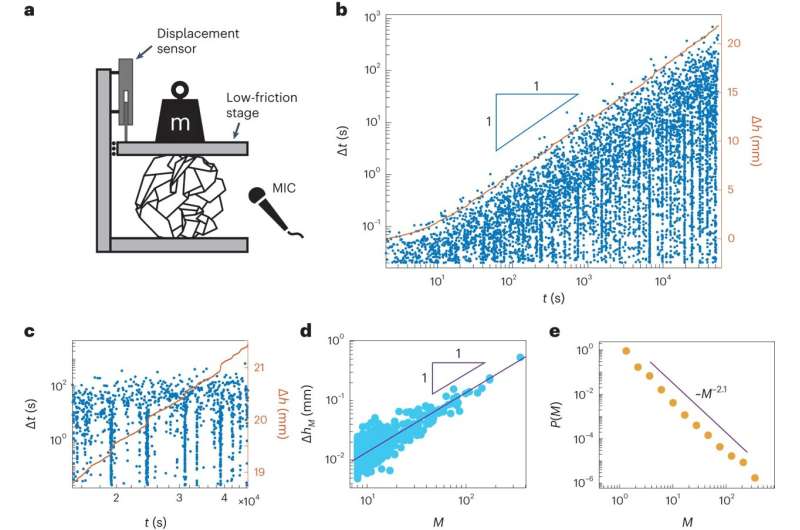
皱巴巴的纸张提供了其他系统所没有的实验途径。在对数弛缓过程中,皱巴巴的薄片发出噪音:断断续续的噼啪声,这源于局部的不稳定——小的、双稳定的区域通过薄片释放压力。该团队意识到,这些吸波槽的不稳定性决定了薄片的机械响应。缓慢的对数弛豫实际上是间歇性的,并通过一系列突然的不稳定性发生。
声发射的统计数据揭示了一个更令人惊讶的结果。皱球的不稳定性不是随机发生的。事实上,它们彼此触发,形成无标度的不稳定性雪崩。“这种情况类似于自组织临界,系统自发地将自己定位在稳定的边缘,各种规模的雪崩出现,没有任何典型的规模,”Shohat解释说。
“但这里有一个转折。系统在展示这些关键雪崩的同时进化。雪崩对应于一个固定的、广泛的分布,但它们跨越更多的时间尺度,随着系统的松弛变得更加稀疏。”
为了进一步了解松弛机制,研究人员采用了代表薄片的无序弹性网络的数值模拟。在该模型中,网络中的每个键都是双稳定的,本质上是一个弹性弹簧,但有两个静止长度。这代表了实验观察到的局域不稳定性。在外力作用下,模拟网络通过突发性、无标度和慢速雪崩进行间歇性压缩,捕获了所有实验观测值。
模拟显示,缓慢的对数弛豫是由一个简单的机制驱动的:在每个压实步骤之前,其中一个键位于不稳定的边缘,接近于在其休息长度之间断裂。这种断裂是由随机过程中的噪声激活的,从而引发不稳定性的雪崩。
每次雪崩之后,触发下一个不稳定的能量屏障会稍微增加,导致穿越时间更长。雪崩之间等待时间的增加会导致动力学的减慢,通常会导致对数松弛。
拉希尼说:“这种机制的简单性表明,它可能与一系列无序系统有关。寻找由缓慢雪崩组成的间歇性松弛的类似特征,可以帮助理解玻璃系统、无定形固体甚至地震的动力学。”


